A 3D Scene Perception Method Based on Uncertainty Modeling
-
摘要: 本文旨在解决多任务场景感知中存在的局限性,包括缺乏对检测、跟踪、建图、定位等任务的状态估计不确定性的系统建模分析。将场景感知任务划分为前景感知和背景感知,前者主要涉及前景目标的检测与跟踪,而后者专注于机器人的定位和建图任务。为了实现对复杂场景的多任务感知,将二者融合于动态贝叶斯网络框架下,将多任务场景感知问题建模为系统状态参数的联合优化估计问题,采用贝叶斯后验概率估计对各系统参数状态进行建模。从LiDAR(激光雷达)传感器的点云测量噪声入手,分析了目标检测与跟踪网络中真值标注和自身姿态估计的不确定性并构建了点云测量及标签的不确定性模型和基于预测置信度的跟踪模型,同时分析了定位误差对建图不确定性及目标跟踪任务的影响,使用迭代扩展卡尔曼滤波对姿态最大后验概率估计进行优化。本文方法可实现复杂大规模动态环境的场景感知,在KITTI和UrbanNav数据集上的实验结果表明,本文方法有效解决了复杂场景下动态目标对环境建图的影响,具有高精度和鲁棒性。Abstract: This paper aims to address limitations in multi-task scene perception, including the lack of system modeling and analysis on the uncertainty in state estimation for tasks such as detection, tracking, mapping, and localization. The scene perception task is divided into foreground and background perception tasks, where the former involves the detection and tracking of foreground objects, and the latter focuses on robot localization and mapping tasks. To achieve multi-task perception in complex scenes, both tasks are integrated within a dynamic Bayesian network framework. The multi-task scene perception problem is modeled as a joint optimization and estimation problem of system state parameters. Bayesian posterior probability estimation is employed to model the state of each system parameter. Starting with the point cloud measurement noises from LiDAR sensors, the uncertainties in ground truth annotation and self-pose estimation in the object detection and tracking network are analyzed, and uncertainty models for point cloud measurements and labels are constructed, along with a tracking model based on prediction confidence. Additionally, the impact of localization errors on mapping uncertainty and target tracking tasks is analyzed. An iterative extended Kalman filter is used to optimize the estimation of the pose's maximum posterior probability. The proposed method achieves scene perception in complex and large-scale dynamic environments. Experimental results on the KITTI and UrbanNav datasets demonstrate its effectiveness in addressing the impact of dynamic targets on environmental mapping in complex scenes, with high accuracy and robustness.
-
多任务场景感知在智能无人系统中扮演着重要的角色,它涉及到对场景中各种元素的综合理解和推理,为系统的决策和规划提供关键信息。通过多任务场景感知,无人系统可以对感兴趣的目标进行检测和分类,对动态物体的状态进行估计,对场景进行语义分割和建图[1]等操作。这些任务相互关联,相互影响,通过综合处理不同任务的结果,系统可以实现更全面、准确的场景理解。
场景感知问题本质上是对环境的建模与对系统状态的优化估计问题。在现有的绝大部分研究中,对这些参数的优化估计往往被分开研究,忽略了它们相互之间的影响。当前研究大多注重分析单一任务的不确定性,很少从多任务的互相关联的角度进行建模。早期的3D目标检测方法忽略了由误检、漏检或标签不可靠等因素引起的检测结果不确定性。为解决此问题,近期的3D目标检测方法提出了不同的解决方案,主要关注标签不确定性[2-3],采用概率性边界框或检测器表示监督不确定性模型,以提高检测性能。同时,一些方法通过设计多损失函数[4]、多输入多输出不确定性估计方法[5],以及开展角变换与预测不确定性建模[6]等方式,有效应对训练中的噪声来提高检测性能。在3D多目标跟踪(MOT)中,对遮挡严重或距离较远的物体进行可靠检测仍具有挑战性。为解决此问题,一些3D MOT方法采用了恒定速度模型[7-8]假设,但在速度剧烈变化或目标连续多帧消失时存在预测误差累积的问题。其他方法使用基于学习的预测器[9],尽管性能优越,但计算量较大。在基于LiDAR的SLAM(同步定位与地图创建)方法中,多数方法[10-16]忽略了激光雷达测量噪声和位姿估计误差带来的地图不确定性。
为解决这一问题,本文将场景感知任务狭义地划分为前景感知和背景感知。在前景感知任务中,主要研究目标检测与运动目标跟踪;在背景感知任务中,主要研究环境建图和定位任务。在已有工作[17-18]的基础上,针对复杂动态场景感知问题,将目标检测、动态物体跟踪、环境建图与机器人定位任务统一在动态贝叶斯网络(DBN)的框架下对其进行建模。同时,对系统的不确定性进行了分析。从激光雷达的点云测量的不确定性建模入手,对该框架下的建图不确定性、目标检测与跟踪不确定性和定位不确定性进行建模,为相关领域的研究提供理论参考。
1. 本文方法(The proposed method)
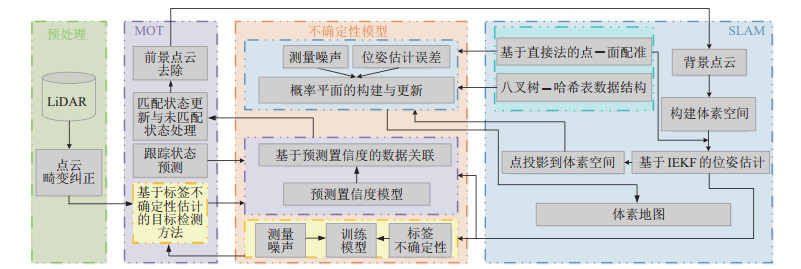
本文方法的系统结构如图 1所示。为了解决目标检测、MOT和SLAM等多任务联合优化求解中的挑战,基于之前提出的DBN框架[17]对这类复杂多变量系统进行建模。系统建模的侧重点在于降低目标检测时LiDAR 3D点云的测量噪声和训练标签不确定性的影响,减少MOT任务中由漏检和不准确的预测状态导致的不可靠的数据关联,和SLAM任务中由3D点云的测量噪声和姿势估计误差导致的局部平面特征的不确定性,以及运动目标导致的建图不一致性问题。通过系统联合建模,进一步提升系统状态估计结果的鲁棒性和精度。
所提出方法的数据处理流程:先对LiDAR获取的原始3D点云进行预处理,通过基于标签不确定性的目标检测方法、恒定加速度(CA)运动模型和扩展卡尔曼滤波(EKF)算法实现基于不确定性模型的跟踪状态的可靠预测与更新,据此对匹配状态进行更新,并通过设置阈值对未匹配的检测和预测状态进行相应处理,最终去除该部分潜在动态目标的点云,减少对SLAM过程的干扰,同时SLAM反馈的精确位置信息也可减小目标运动预测的不确定性。为了消除复杂场景下运动目标对建图一致性及位姿估计的影响,仅用静态背景点云进行建图匹配与位姿估计。具体来说,通过概率自适应方法构建基于静态点云的体素地图,通过不确定性模型中平面特征参数的构建与更新,基于直接法点-面配准和动态八叉树实时生成并管理体素地图。同时,通过IEKF优化后的姿态估计与体素内平面特征的不确定性参数来调节目标检测与跟踪中数据关联模型的权重计算,提高跟踪鲁棒性。在目标检测、跟踪和SLAM等多个任务的协同过程中,不同任务的时间约束和优先级存在细微差异,需要进行调度协调。前景目标检测和跟踪任务对环境建图有最强的实时反馈需求,恰恰定位模块中的位姿估计输出又是目标跟踪任务中传感器运动模型的输入,因此这两者需要实时交互,而建图输出则可以稍滞后。因此,在方法实现上,采用基于时间窗和优先级的任务调度策略,保证目标检测和跟踪、以及位姿估计的实时性,同时通过适当的缓冲接收建图任务的反馈结果。
1.1 基于DBN的多任务感知联合建模
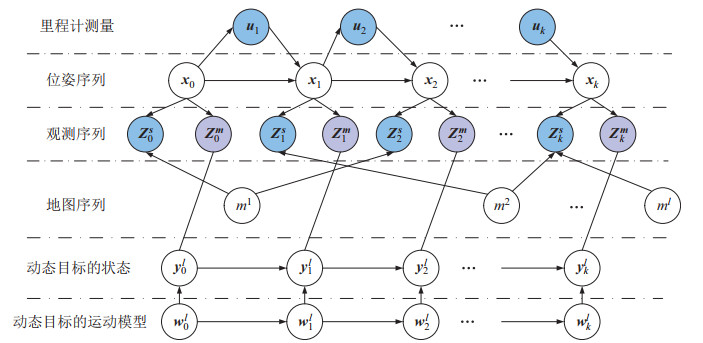
图 2为基于DBN的多任务环境感知概率图模型。
假设系统是一个典型的非线性动态系统,用离散状态空间模型表示,则有:
$$ \begin{equation} \begin{aligned} {\mathit{\boldsymbol{x}}}_{k} & ={\mathit{\boldsymbol{f}}}({\mathit{\boldsymbol{x}}}_{k-1}, {\mathit{\boldsymbol{u}}}_{k})+{\mathit{\boldsymbol{\upsilon}}}_{k} \\ {\mathit{\boldsymbol{z}}}_{k} & ={\mathit{\boldsymbol{h}}}({\mathit{\boldsymbol{x}}}_{k})+{\mathit{\boldsymbol{\omega}}}_{k} \end{aligned} \end{equation} $$ (1) 其中$ \mathit{\boldsymbol{f}}(\cdot) $和$ \mathit{\boldsymbol{h}}(\cdot) $分别为非线性状态转移模型和观测模型,$ \mathit{\boldsymbol{\upsilon}}_{k} $和$ \mathit{\boldsymbol{\omega}}_{k} $为噪声向量,假设它们是高斯的、时间不相关的、零均值的。从传统SLAM任务的角度,假设机器人的轨迹可以用一系列随机变量表示如下:
$$ \begin{align} {\mathit{\boldsymbol{X}}}_{1:k} \triangleq [ {\mathit{\boldsymbol{x}}}_{0}, {\mathit{\boldsymbol{x}}}_{1}, \cdots, {\mathit{\boldsymbol{x}}}_{k}]=[ {\mathit{\boldsymbol{x}}}_{0:k-1}, {\mathit{\boldsymbol{x}}}_{k}] \end{align} $$ (2) 同样,使
$$ \begin{align} {\mathit{\boldsymbol{Z}}}_{1:k} & \triangleq [ {\mathit{\boldsymbol{z}}}_{0}, {\mathit{\boldsymbol{z}}}_{1}, \cdots, {\mathit{\boldsymbol{z}}}_{k}]=[ {\mathit{\boldsymbol{z}}}_{0:k-1}, {\mathit{\boldsymbol{z}}}_{k}] \end{align} $$ (3) $$ \begin{align} {\mathit{\boldsymbol{U}}}_{1:k} & \triangleq [ {\mathit{\boldsymbol{u}}}_{0}, {\mathit{\boldsymbol{u}}}_{1}, \cdots, {\mathit{\boldsymbol{u}}}_{k}]=[ {\mathit{\boldsymbol{u}}}_{0:k-1}, {\mathit{\boldsymbol{u}}}_{k}] \end{align} $$ (4) 分别表示环境的观测值和里程计的测量结果。离散时间索引由变量$ k $表示,地图$ {\mathit{\boldsymbol{M}}} $由$ l $个特征组成。从贝叶斯优化估计的角度,SLAM问题的求解等价于在给定所有测量值和初始位姿$ {\mathit{\boldsymbol{x}}}_{0} $的条件下,求解机器人轨迹$ {\mathit{\boldsymbol{X}}}_{1:k} $和环境地图$ {\mathit{\boldsymbol{M}}} $的后验概率估计问题$ p({\mathit{\boldsymbol{X}}}_{1:k}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{U}}}_{1:k}, {\mathit{\boldsymbol{Z}}}_{1:k}, {\mathit{\boldsymbol{x}}}_{0}) $。假设SLAM过程为马尔可夫过程,如果环境为静态的,则SLAM问题的迭代后验概率估计可表示为
$$ \begin{align} & \underbrace{p({\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{Z}}}_{k}, {\mathit{\boldsymbol{U}}}_{k})}_{\text{posterior at time }\;k}\\ \propto &\underbrace{p({\mathit{\boldsymbol{z}}}_{k} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}})}_{\text{observation part}}\cdot \\ & \underbrace{\int {p({\mathit{\boldsymbol{x}}}_{k} |} {\mathit{\boldsymbol{x}}}_{k-1}, {\mathit{\boldsymbol{u}}}_{k})\underbrace{p({\mathit{\boldsymbol{x}}}_{k-1}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{Z}}}_{k-1}, {\mathit{\boldsymbol{U}}}_{k-1})}_{\text{posterior at time }\;k-1}{\rm d}{\mathit{\boldsymbol{x}}}_{k-1}}_{\text{prediction part}} \end{align} $$ (5) 式(5) 表示了静态环境假设条件下的SLAM模型,这里的地图特征点对应于背景点云部分,其观测只与机器人当前的位姿和特征点的状态有关。
在上述传统SLAM建模的基础上,针对复杂动态场景,将式(5) 扩展到存在运动目标的动态环境中,完成前景目标的感知任务。为了描述此时的系统状态,需要添加一些新的随机变量对其进行表示,如下所示:
$$ \begin{equation} \begin{aligned} {\mathit{\boldsymbol{Y}}}_{k} & \triangleq [ {\mathit{\boldsymbol{y}}}_{k}^{1}, {\mathit{\boldsymbol{y}}}_{k}^{2}, \cdots, {\mathit{\boldsymbol{y}}}_{k}^{n}] \\ {\mathit{\boldsymbol{W}}}_{k} & \triangleq [ {\mathit{\boldsymbol{w}}}_{k}^{1}, {\mathit{\boldsymbol{w}}}_{k}^{2}, \cdots, {\mathit{\boldsymbol{w}}}_{k}^{n}] \end{aligned} \end{equation} $$ (6) 式中,$ {\mathit{\boldsymbol{Y}}}_{k} $为运动目标的状态,$ {\mathit{\boldsymbol{W}}}_{k} $为运动目标的运动模型。
如图 2所示,SLAM任务的地图表示为$ {\mathit{\boldsymbol{m}}} \triangleq [ m^{1}, m^{2}, \cdots, m^{l}] $,对应的观测值定义为$ {\mathit{\boldsymbol{Z}}}_{0:k}^{{\mathit{\boldsymbol{s}}}} \triangleq [ {\mathit{\boldsymbol{z}}}_{0}^{{\mathit{\boldsymbol{s}}}}, {\mathit{\boldsymbol{z}}}_{1}^{{\mathit{\boldsymbol{s}}}}, \cdots, {\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{s}}}}]=[ {\mathit{\boldsymbol{z}}}_{0:k-1}^{{\mathit{\boldsymbol{s}}}}, {\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{s}}}} ] $,前景目标的状态$ {\mathit{\boldsymbol{Y}}}_{k} $、运动模型$ {\mathit{\boldsymbol{W}}}_{k} $以及观测值$ {\mathit{\boldsymbol{Z}}}_{0:k}^{{\mathit{\boldsymbol{m}}}} \triangleq [ {\mathit{\boldsymbol{z}}}_{0}^{{\mathit{\boldsymbol{m}}}}, {\mathit{\boldsymbol{z}}}_{1}^{{\mathit{\boldsymbol{m}}}}, \cdots, {\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{m}}}}]=[ {\mathit{\boldsymbol{z}}}_{0:k-1}^{{\mathit{\boldsymbol{m}}}}, {\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{m}}}} ] $。图中,蓝色节点包含里程计测量值$ {\mathit{\boldsymbol{u}}}_{i} $($ i=1, \cdots, k $),观测序列节点$ ({{\mathit{\boldsymbol{z}}}_{i}^{{\mathit{\boldsymbol{s}}}}, {\mathit{\boldsymbol{z}}}_{i}^{{\mathit{\boldsymbol{m}}}}}) $中$ {\mathit{\boldsymbol{s}}} $表示对背景点云的观测,$ {\mathit{\boldsymbol{m}}} $表示对前景目标的观测,用紫色显示。这些蓝色节点表示显式状态。无色节点表示隐藏或隐式状态,这些状态从显式状态中衍生出来。
为了实现多任务感知的系统状态优化估计建模,将观测值分解为2个独立的部分,背景和前景部分。其中前景主要包括场景中的各类前景目标(静态的和运动的),背景部分主要是去除前景目标之后的剩余部分。于是可得到:
$$ \begin{align} &{\mathit{\boldsymbol{z}}}_{k} \triangleq {\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{s}}}} +{\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{m}}}}\\ \Rightarrow & {\mathit{\boldsymbol{z}}}_{0:k} ={\mathit{\boldsymbol{z}}}_{0:k}^{{\mathit{\boldsymbol{s}}}} +{\mathit{\boldsymbol{z}}}_{0:k}^{{\mathit{\boldsymbol{m}}}} \\ \Rightarrow & p({\mathit{\boldsymbol{z}}}_{k} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}, {\mathit{\boldsymbol{y}}}_{k}) =p({\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{s}}}} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}, {\mathit{\boldsymbol{y}}}_{k})p({\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{m}}}} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}, {\mathit{\boldsymbol{y}}}_{k}) \end{align} $$ (7) 其中,$ {\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{s}}}} $表示背景地图点的观测值,$ {\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{m}}}} $表示前景目标的观测值。式(7) 定义了联合观测概率。其中:
$$ \begin{align} p({\mathit{\boldsymbol{z}}}_{k} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}, {\mathit{\boldsymbol{y}}}_{k})& =p({\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{s}}}} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}, {\mathit{\boldsymbol{y}}}_{k})p({\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{m}}}} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}, {\mathit{\boldsymbol{y}}}_{k}) \\ & =p({\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{s}}}} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}})p({\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{m}}}} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{y}}}_{k}) \end{align} $$ (8) 基于上述假设,基于贝叶斯后验概率估计的多任务环境感知系统状态参数的优化估计定义如下:
$$ \begin{align} p({\mathit{\boldsymbol{Y}}}_{k}, {\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{U}}}_{k}, {\mathit{\boldsymbol{Z}}}_{k})& \propto p({\mathit{\boldsymbol{Z}}}_{k} |{\mathit{\boldsymbol{Y}}}_{k}, {\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}, {\mathit{\boldsymbol{U}}}_{k}, {\mathit{\boldsymbol{Z}}}_{k-1}) \cdot \\ &\quad p({\mathit{\boldsymbol{Y}}}_{k}, {\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{Z}}}_{k-1}, {\mathit{\boldsymbol{U}}}_{k}) \end{align} $$ (9) 其中,$ p({\mathit{\boldsymbol{Z}}}_{k} |{\mathit{\boldsymbol{Y}}}_{k}, {\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}, {\mathit{\boldsymbol{U}}}_{k}, {\mathit{\boldsymbol{Z}}}_{k-1}) $为观测概率,与式(8) 中相同。$ p({\mathit{\boldsymbol{Y}}}_{k}, {\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{Z}}}_{k-1}, {\mathit{\boldsymbol{U}}}_{k}) $为预测概率,可如下分解:
$$ \begin{align} p({\mathit{\boldsymbol{Y}}}_{k}, {\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{Z}}}_{k-1}, {\mathit{\boldsymbol{U}}}_{k}) & =p({\mathit{\boldsymbol{Y}}}_{k} |{\mathit{\boldsymbol{Z}}}_{k-1}, {\mathit{\boldsymbol{U}}}_{k}) \cdot \\ &\quad p({\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{Z}}}_{k-1}, {\mathit{\boldsymbol{U}}}_{k}) \end{align} $$ (10) 用式(8)(10) 代替式(9) 中对应部分,得到式(11):
$$ \begin{align} & p({\mathit{\boldsymbol{Y}}}_{k}, {\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{U}}}_{k}, {\mathit{\boldsymbol{Z}}}_{k}) \\ \propto& p({\mathit{\boldsymbol{Z}}}_{k} |{\mathit{\boldsymbol{Y}}}_{k}, {\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}, {\mathit{\boldsymbol{U}}}_{k}, {\mathit{\boldsymbol{Z}}}_{k-1}) \cdot p({\mathit{\boldsymbol{Y}}}_{k}, {\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{Z}}}_{k-1}, {\mathit{\boldsymbol{U}}}_{k}) \\ =&\underbrace{p({\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{s}}}} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}})p({\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{M}}}|{\mathit{\boldsymbol{Z}}}_{k-1}, {\mathit{\boldsymbol{U}}}_{k})}_{\text{static SLAM}} \cdot \\ &\quad \underbrace{p({\mathit{\boldsymbol{z}}}_{k}^{{\mathit{\boldsymbol{m}}}} |{\mathit{\boldsymbol{x}}}_{k}, {\mathit{\boldsymbol{y}}}_{k})p({\mathit{\boldsymbol{Y}}}_{k} |{\mathit{\boldsymbol{Z}}}_{k-1}, {\mathit{\boldsymbol{U}}}_{k})}_{\text{tracking}} \end{align} $$ (11) 由式(11) 可知,多任务感知问题的联合后验概率由传统的静态SLAM和前景目标跟踪的后验概率组成。值得注意的是,前景中运动目标的检测与跟踪,和背景的错误分类,也会降低SLAM的性能。为此,可将背景点云的SLAM与前景目标检测以迭代的方式执行,SLAM输出的位姿估计影响运动目标的检测与跟踪,反之,可靠的前景目标跟踪,对SLAM的建图一致性直接产生影响。本文采用基于预测置信度的数据关联模型与基于EKF的方法来估计MOT的后验概率。
1.2 基于卡尔曼滤波的前景感知建模
前景3D MOT问题定义如下:将检测到的状态$ {\mathit{\boldsymbol{D}}}_{t} $与根据之前完整跟踪状态$ {\mathit{\boldsymbol{T}}}_{t-1} $估计出的预测状态$ \hat{\mathit{\boldsymbol{T}}}_{t} $相关联,执行匹配状态更新和未匹配状态处理以获得新的跟踪状态$ {\mathit{\boldsymbol{T}}}_{t}^{*} $。其中,$ {\mathit{\boldsymbol{T}}}_{t-1} $包括之前跟踪状态$ {\mathit{\boldsymbol{T}}}_{t-1}^{*} $和之前暂时错过检测的预测状态$ \mathit{\boldsymbol{T}}'_{t-1} $。这些状态的具体定义如下:
1) 检测状态$ {\mathit{\boldsymbol{D}}}_{t} $
在基于检测的跟踪框架中,采用基于标签不确定性估计的目标检测方法选取候选对象。检测结果由3D边界框、对应点云特征和检测置信度组成。其中,检测置信度由检测器直接输出,点云特征由检测器主干网提取。为了估计真实物体的运动,所有检测到的3D边界框都要被转换到全局坐标系下。在离散时间$ t $时刻,这些检测状态表示为
$$ \begin{align} {\mathit{\boldsymbol{D}}}_{t} =[ {\mathit{\boldsymbol{D}}}_{t}^{i}]_{i=1}^{N_{t}^{\rm D}} \subset \mathbb{R}^{W^{D}\times 1} \end{align} $$ (12) 其中,$ N_{t}^{\rm D} $是在离散时间$ t $时刻的检测状态总数,$ W^{\rm D} $是检测状态的维度。$ {\mathit{\boldsymbol{D}}}_{t}^{i} $是第$ i $个目标在离散时间$ t $时刻的检测状态,定义为
$$ \begin{align*} {\mathit{\boldsymbol{D}}}_{t}^{i} =[ x_{t}^{i}, y_{t}^{i}, z_{t}^{i}, w_{t}^{i}, h_{t}^{i}, l_{t}^{i}, \alpha_{t}^{i}, f_{t}^{1, i}, \cdots, f_{t}^{n, i} ]^{\rm T} \end{align*} $$ 其中,$ x $、$ y $、$ z $为其全局坐标值,$ w $、$ h $、$ l $是该目标的宽度、高度和长度,$ \alpha $是方向角,$ f $为提取的点云特征。
2) 前一时刻完整跟踪状态$ {\mathit{\boldsymbol{T}}}_{t-1} $
跟踪器还需要输入一组之前的完整跟踪状态$ {\mathit{\boldsymbol{T}}}_{t-1} $,它由之前跟踪状态$ {\mathit{\boldsymbol{T}}}_{t-1}^{*} $和之前暂时错过检测的预测状态$ \mathit{\boldsymbol{T}}'_{t-1} $组成,即$ {\mathit{\boldsymbol{T}}}_{t-1} =[ {\mathit{\boldsymbol{T}}}_{t-1}^{*}, \mathit{\boldsymbol{T}}'_{t-1} ] $。每个完整跟踪状态包括沿坐标轴的速度和加速度,以实现更准确的运动估计。在离散时间$ t-1 $时刻的完整跟踪状态可表示为
$$ \begin{align} {\mathit{\boldsymbol{T}}}_{t-1} =[ {\mathit{\boldsymbol{T}}}_{t-1}^{j}, \cdots ]_{j=1}^{N_{t-1}^{\rm T}} \in \mathbb{R}^{W^{\rm T}\times 1} \end{align} $$ (13) 其中,$ N_{t-1}^{\rm T} $和$ W^{\rm T} $分别表示之前完整跟踪状态的总数和维度。并且,$ {\mathit{\boldsymbol{T}}}_{t-1}^{j} $定义为$ {\mathit{\boldsymbol{T}}}_{t-1}^{j} = [x_{t-1}^{j}, y_{t-1}^{j}, $ $ z_{t-1}^{j}, $ $ v_{t-1}^{x, j}, $ $ v_{t-1}^{y, j}, $ $ v_{t-1}^{z, j}, $ $ a_{t-1}^{x, j}, $ $ a_{t-1}^{y, j}, $ $ a_{t-1}^{z, j}, $ $ w_{t-1}^{j}, $ $ h_{t-1}^{j}, $ $ l_{t-1}^{j}, $ $ \alpha_{t-1}^{j}, $ $ f_{t-1}^{1, j}, $ $ \cdots, f_{t-1}^{n, j} ]^{\rm T} $,$ v $和$ a $分别为沿坐标轴的速度和加速度,表示第$ j $个目标在离散时间$ t-1 $时刻的完整跟踪状态。
3) 预测状态$ \hat{\mathit{\boldsymbol{T}}}_{t} $
为了执行鲁棒的数据关联,采用之前的完全跟踪状态来估计$ t $时刻一组可能的当前状态。预测状态的维数与之前的完整跟踪状态相同。因此,一组预测状态可表示为
$$ \begin{align} \hat{\mathit{\boldsymbol{T}}}_{t} =[ \hat{\mathit{\boldsymbol{T}}}_{t}^{j}, \cdots]_{j=1}^{N_{t-1}^{\rm T}} \in \mathbb{R}^{W^{\rm T}\times 1} \end{align} $$ (14) 式中,$ \hat{\mathit{\boldsymbol{T}}}_{t}^{j} $为离散时间$ t $时刻第$ j $个完全跟踪状态的预测状态。具体而言,预测状态是根据前一时刻的完整跟踪状态,利用恒定加速度模型进行状态演化而得到的。检测状态是当前时刻传感器观测得到的。将两者关联的目的是找到前一时刻被跟踪的目标在当前时刻的最新状态。
1.3 多任务感知不确定性建模
1.3.1 目标检测的不确定性
目标检测性能对基于检测的MOT算法的实现具有十分重要的影响。为了保证算法可靠性,同时将LiDAR测量噪声所导致的点的不确定性以及标签不确定性纳入目标检测不确定性模型的考虑中。
参考其他工作[19]中对LiDAR传感器本身测量噪声的分析,设某个目标所属的点云集合表示为$ {}^{L}O=\{{{}^{L}{\mathit{\boldsymbol{o}}}_{i}}\}_{i=1}^{n} $,局部LiDAR坐标系下LiDAR点$ {}^{L}o_{i} $的不确定性包含测距不确定性和方位不确定性。设$ {\mathit{\boldsymbol{u}}}_{i} \in S^{2} $是测得的方位,$ S^{2} $表示2维球面上的对称群,$ \boldsymbol\delta_{{\mathit{\boldsymbol{u}}}_{i}} $是$ {\mathit{\boldsymbol{u}}}_{i} $在切平面上的方位噪声,服从$ {\mathcal N}({\mathit{\boldsymbol{0}}}_{2\times 1}, {\mathit{\boldsymbol{\varSigma}}}_{{\mathit{\boldsymbol{u}}}_{i}}) $分布,$ v_{i} $是所测距离,$ \delta_{v_{i}} $是测距噪声,服从$ {\mathcal N}(0, {\varSigma}_{v_{i}}) $分布。则点$ {}^{L}{o}_{i} $的噪声$ \boldsymbol \delta_{^{L}{\mathit{\boldsymbol{o}}}_{i}} $及其协方差$ \mathit{\boldsymbol{\varSigma}}_{^{L}{\mathit{\boldsymbol{o}}}_{i}} $如式(15) 所示:
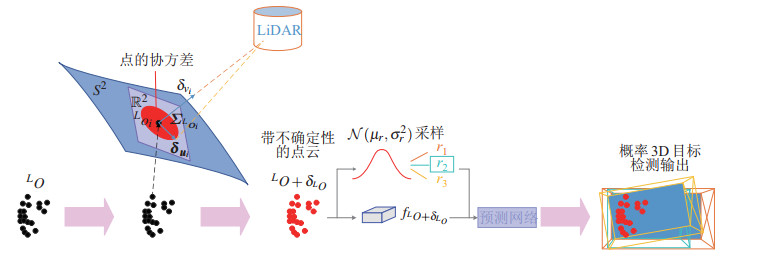
$$ \begin{equation} \begin{aligned} \boldsymbol\delta_{^{L}{\mathit{\boldsymbol{o}}}_{i}} & =\underbrace{[ {\mathit{\boldsymbol{u}}}_{i} -v_{i} \lfloor {{\mathit{\boldsymbol{u}}}_{i}} \rfloor_{\wedge} {\mathit{\boldsymbol{N}}}({{\mathit{\boldsymbol{u}}}_{i}})]}_{{\mathit{\boldsymbol{A}}}_{i}} \begin{bmatrix} {v_{i}} \\ {{\mathit{\boldsymbol{u}}}_{i}} \end{bmatrix}\sim {\mathcal N}({\mathit{\boldsymbol{0}}}, \boldsymbol \varSigma_{^{L}{\mathit{\boldsymbol{o}}}_{i}}) \\ \boldsymbol \varSigma_{^{L}{\mathit{\boldsymbol{o}}}_{i}} & ={\mathit{\boldsymbol{A}}}_{i} \begin{bmatrix} {\varSigma_{v_{i}}} & {{\mathit{\boldsymbol{0}}}_{1\times 2}} \\ {{\mathit{\boldsymbol{0}}}_{2\times 1}} & {\boldsymbol \varSigma_{{\mathit{\boldsymbol{u}}}_{i}}} \end{bmatrix}\mathit{\boldsymbol{A}}_{i}^{\rm T} \end{aligned} \end{equation} $$ (15) 其中$ {\mathit{\boldsymbol{N}}}({{\mathit{\boldsymbol{u}}}_{i}})=[ {\mathit{\boldsymbol{N}}}_{1}, {\mathit{\boldsymbol{N}}}_{2}]\in \mathbb{R}^{3\times 2} $是$ {\mathit{\boldsymbol{u}}}_{i} $处切平面的标准正交基,$ \lfloor\; \rfloor_{\wedge} $表示映射叉乘的斜对称矩阵。由此,基于每个点及其协方差,构建标签不确定性模型。使$ G $表示$ {}^{L}O $的标注真值边界框,将一个目标的标注真值标签的不确定性表述为该目标的潜在边界框的多样性,这种多样性可以用潜在边界框分布的方差来定量测量。首先,对基于点云$ {}^{L}O $的潜在边界框的分布进行建模,考虑到噪声问题,将其表示为$ p({G|{}^{L}O+\delta_{^{L}O}}) $。具体来说,基于贝叶斯定理,同时引入一个中间变量$ r $将条件分布写成:
$$ \begin{align} &p({G|{}^{L}O+\delta_{^{L}O}}) \\ =&\int_r p({G|r, {}^{L}O+\delta_{^{L}O}}) p(r|{}^{L}O+\delta_{^{L}O}){\rm d}z \end{align} $$ (16) 其中,假设先验分布$ p({r|{}^{L}O+\delta_{^{L}O}}) $服从参数化为$ ({\mu_{r}, \sigma_{r}^{2}}) $的多元高斯分布。先验网络利用输入点云$ {}^{L}O+\delta_{^{L}O} $预测$ ({\mu_{r}, \sigma_{r}}) $的值,并使用上下文编码器提取点云的几何特征表示$ f_{^{L}O+\delta_{^{L}O}} $,它与从$ {\mathcal N}({\mu_{r}, \sigma_{r}^{2}}) $中采样的不同的$ r $连接起来,输入到预测网络中,由此求得边界框分布$ p({G|r, {}^{L}O+\delta_{^{L}O}}) $。具体的采样方法为蒙特卡洛方法[20],建模过程如图 3所示。先验网络与上下文编码器网络架构可参考文[3]。
1.3.2 MOT任务的不确定性建模
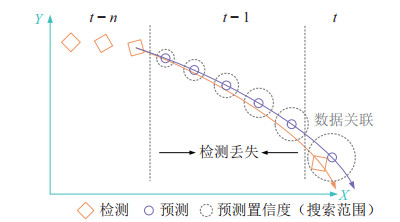
由于预测状态和检测状态之间存在一定的偏差,因此不能简单地进行匹配。为实现可靠的数据关联,考虑对MOT中目标轨迹的固有不确定性进行建模,利用完整的点云特征进行跟踪并实现可靠的数据关联。首先结合点云中目标的几何形状、外观和运动特征构造代价模型$ \mathit{\boldsymbol{C}}_{t} $[3],在此基础上构建基于预测置信度的数据关联不确定性模型,由此提高数据关联的可靠性。为了获得目标对应关系,传统的MOT方法大多采用关联策略直接对检测和预测步骤进行数据关联,但缺乏对预测质量的考虑。由于预测的结果并不总是准确的,特别是对于连续多帧被检测器遗漏的目标。在没有状态更新的情况下,预测误差可能会累积。具体操作中,适当扩大目标的搜索区域,并在数据关联环节充分考虑不确定性因素,从而提高关联的可靠性。因此,将MOT的不确定性模型设计为基于预测置信度的数据关联模型,其具体说明如图 4所示。
1) 预测置信度$ \beta $
为了将预测质量纳入数据关联的考虑范围,对每个预测状态构建了预测置信度$ \beta $,如下所示:
$$ \begin{align} \hat{\beta}_{t}^{j} =\beta_{t-1}^{j} -\mu \beta_{t-1}^{j} \end{align} $$ (17) 其中,$ \mu \in (0, 1] $,$ \mu $是调整预测置信度对数据关联整体影响的参数,在训练数据集上验证确定。$ \beta_{t-1}^{j} $为离散时间$ t-1 $时刻的预测置信度。预测置信度$ \beta \in (0, 1 ] $且初始化为1,后续通过式(17) 进行更新。当检测器漏掉一个目标时,预测的置信度会降低,数据关联对应的搜索范围就会被扩大。通过构建预测置信度,可以自适应地调整数据关联的搜索范围。
2) 预测置信度引导的数据关联$ {\mathit{\boldsymbol{\xi}}}_{t} $
为了解决上述数据关联中未充分考虑预测质量的问题,提出了基于预测置信度的数据关联模型,它考虑了预测误差,并灵活地调整搜索范围,以执行更鲁棒的数据关联。首先,为了关联离散时间$ t $处的检测状态和预测状态,引入了一个预测置信度引导的关联矩阵$ \mathit{\boldsymbol{\xi}}_{t} $,该关联矩阵由代价模型$ \mathit{\boldsymbol{C}}_{t} $和预测置信度式(17) 计算得到:
$$ \begin{align} {\mathit{\boldsymbol{\xi}}}_{t} =\begin{bmatrix} {\beta_{t}^{1} {\mathcal C}_{t}^{1, 1}} & \cdots & {\beta_{t}^{N_{t-1}^{\rm T}} {\mathcal C}_{t}^{1, N_{t-1}^{\rm T}}} \\ \vdots & \ddots & \vdots \\ {\beta_{t}^{1} {\mathcal C}_{t}^{N_{t}^{\rm D}, 1}} & \cdots & {\beta_{t}^{N_{t-1}^{\rm T}} {\mathcal C}_{t}^{N_{t}^{\rm D}, N_{t-1}^{\rm T}}} \end{bmatrix} \end{align} $$ (18) 最后采用贪婪算法作为关联匹配策略来获得目标对应关系,包括匹配的跟踪状态以及不匹配的检测和预测状态。
1.3.3 建图的不确定性模型
为了对建图不确定性进行分析,本文的建图方法基于现有较领先的FAST-LIO2算法[10]进行了扩展,通过构建概率平面模型对地图点的不确定性进行建模,采用概率自适应方法将直接法点云配准中拟合的实际平面改为概率平面,并由此提高算法对LiDAR点云的不规则性和不同环境的适应性。
本方法采用体素表示形式来构建地图,并在体素空间的背景下构建不确定性模型。假定在体素空间中,体素地图的每个体素都包含一个局部概率平面,即采用平面特征的形式实现后续LiDAR点的直接配准。由于平面特征是由落在该体素格内的点估计得出,因此与点相关的任何噪声都会影响平面估计的结果。其中,体素图及其平面特征都是在世界坐标系下表示的,则生成的点及其噪声也应在世界坐标系下进行研究。据此需要考虑2个噪声源:一个是由LiDAR传感器本身造成的原始点测量噪声(目标检测考虑检测物体的点噪声,本部分考虑背景点噪声,原理相同),此时在局部LiDAR坐标系下;另一个是将局部LiDAR坐标系下的点转换到世界坐标系下时产生的LiDAR位姿估计误差。在此基础上推导出点模型及平面模型。
1) 点的不确定性模型
点的不确定性模型与目标检测不确定性模型中对点噪声的建模相同,参考式(15)。不同的是,检测跟踪部分的前景LiDAR点云在建图时已经被移除,不需要转换坐标系,只需要考虑LiDAR传感器测量噪声。而利用背景点云进行建图时,关于点$ {}^{L}o_{i} $的位置,不仅要考虑LiDAR测量噪声,还需要通过估计的位姿$ {}_{L}^{W} {\mathit{\boldsymbol{P}}}=({{}_{L}^{W} {\mathit{\boldsymbol{R}}}, {}_{L}^{W} {\mathit{\boldsymbol{t}}}})\in SE(3) $将其投影到世界坐标系下,位姿估计的不确定性为$ ({\mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{R}}}}, \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{t}}}}}) $,则可通过下式进行坐标系变换:
$$ \begin{align} {}^{W}{\mathit{\boldsymbol{o}}}_{i} ={}_{L}^{W} {\mathit{\boldsymbol{R}}}\; {}^{L}{\mathit{\boldsymbol{o}}}_{i} +{}_{L}^{W} {\mathit{\boldsymbol{t}}} \end{align} $$ (19) 由此可得转换后的点$ ^{W}o_{i} $的协方差为
$$ \begin{align} \mathit{\boldsymbol{\varSigma}}_{^{W}{\mathit{\boldsymbol{o}}}_{i}} = {}_{L}^{W} {\mathit{\boldsymbol{R}}}\mathit{\boldsymbol{\varSigma}}_{^{L}{\mathit{\boldsymbol{o}}}_{i}} {}_{L}^{W} {\mathit{\boldsymbol{R}}}^{\rm T} + {}_{L}^{W} {\mathit{\boldsymbol{R}}}\lfloor {{}^{L}{\mathit{\boldsymbol{o}}}_{i}} \rfloor_{\wedge} \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{R}}}} \lfloor {{}^{L}{\mathit{\boldsymbol{o}}}_{i}} \rfloor_{\wedge}^{\rm T}\; {}_{L}^{W} {\mathit{\boldsymbol{R}}}^{\rm T}+\mathit{\boldsymbol{\varSigma}}_{t} \end{align} $$ (20) 其中,$ \mathit{\boldsymbol{\varSigma}}_{\mathit{\boldsymbol{R}}} $代表$ {}_{L}^{W} {\mathit{\boldsymbol{R}}} $的不确定性,$ \mathit{\boldsymbol{\varSigma}}_{\mathit{\boldsymbol{t}}} $代表$ {}_{L}^{W} \mathit{\boldsymbol{t}} $的不确定性。需要注意的是,在不同的位置协方差的值有较大差异,这是因为各点的噪声中距离较近的点以距离噪声为主,而距离较远的点以方位噪声为主。LiDAR点的不确定性分析是建立在平面特征分析的基础上,其模型如图 5所示。
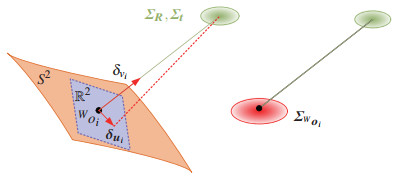
2) 局部平面的不确定性模型
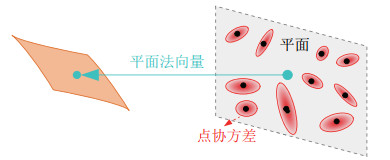
模型如图 6所示。若一个平面特征由一组LiDAR点$ ^{W}o_{i} $($ i=1, \cdots, N $)组成,根据点的不确定性,体素内局部平面中心$ \overline o $的位置及各点的协方差矩阵$ {\mathit{\boldsymbol{A}}} $可表示为
$$ \begin{align} \overline{{\mathit{\boldsymbol{o}}}} =\frac{1}{N}\sum\limits_{i=1}^N {}^{W}{\mathit{\boldsymbol{o}}}_{i} , \quad \mathit{\boldsymbol{A}}=\frac{1}{N}\sum\limits_{i=1}^N ({{}^{W}{\mathit{\boldsymbol{o}}}_{i} -\overline{{\mathit{\boldsymbol{o}}}}}) ({{}^{W}{\mathit{\boldsymbol{o}}}_{i} -\overline{{\mathit{\boldsymbol{o}}}}})^{\rm T} \end{align} $$ (21) 由此可利用与矩阵$ {\mathit{\boldsymbol{A}}} $的最小特征值相关的特征向量表示该平面的法向量$ {\mathit{\boldsymbol{n}}} $,令$ \mathit{\boldsymbol{c}}=\overline{\mathit{\boldsymbol{o}}} $,$ {\mathit{\boldsymbol{c}}} $和$ {\mathit{\boldsymbol{A}}} $都依赖于$ ^{W}{\mathit{\boldsymbol{o}}}_{i} $,则可将平面参数$ ({\mathit{\boldsymbol{n}}}, {\mathit{\boldsymbol{c}}}) $表示为$ ^{W}{\mathit{\boldsymbol{o}}}_{i} $的函数:
$$ \begin{align} [ {\mathit{\boldsymbol{n}}}, {\mathit{\boldsymbol{c}}}]^{\rm T}={\mathit{\boldsymbol{f}}}( {}^{W}{\mathit{\boldsymbol{o}}}_{1}, {}^{W}{\mathit{\boldsymbol{o}}}_{2}, \cdots, {}^{W}{\mathit{\boldsymbol{o}}}_{N}) \end{align} $$ (22) 每个LiDAR点$ ^{W}o_{i} $的噪声$ \boldsymbol\delta_{^{W}{\mathit{\boldsymbol{o}}}_{i}} $服从$ {\mathcal N}(\mathit{\boldsymbol{0}}_{3\times 1}, \ \mathit{\boldsymbol{\varSigma}}_{^{W}{\mathit{\boldsymbol{o}}}_{i}}) $,由此可计算平面参数待估计的真实值:
$$ \begin{align} [ {\mathit{\boldsymbol{n}}}^{\rm gt}, {\mathit{\boldsymbol{c}}}^{\mathrm{gt}}]^{\rm T}& ={\mathit{\boldsymbol{f}}}({}^{W}{\mathit{\boldsymbol{o}}}_{1} +{\mathit{\boldsymbol{\boldsymbol\delta}}}_{^{W}{\mathit{\boldsymbol{o}}}_{1}}, {}^{W}{\mathit{\boldsymbol{o}}}_{2} +{\mathit{\boldsymbol{\boldsymbol\delta}}}_{^{W}{\mathit{\boldsymbol{o}}}_{2}}, \cdots, \\ &\quad {}^{W}{\mathit{\boldsymbol{o}}}_{N} +{\mathit{\boldsymbol{\boldsymbol\delta}}}_{^{W}{\mathit{\boldsymbol{o}}}_{N}} ) \\ & \approx [ {\mathit{\boldsymbol{n}}}, {\mathit{\boldsymbol{c}}}]^{\rm T}+\sum\limits_{i=1}^N \frac{\partial {\mathit{\boldsymbol{f}}}}{\partial {}^{W}{\mathit{\boldsymbol{o}}}_{i}} {\mathit{\boldsymbol{\boldsymbol\delta}}}_{^{W}{\mathit{\boldsymbol{o}}}_{i}} \end{align} $$ (23) 其中,$ \dfrac{\partial {\mathit{\boldsymbol{f}}}}{\partial {}^{W}{\mathit{\boldsymbol{o}}}_{i}} =\left[ \dfrac{\partial {\mathit{\boldsymbol{n}}}}{\partial {}^{W}{\mathit{\boldsymbol{o}}}_{i}} , \dfrac{\partial {\mathit{\boldsymbol{c}}}}{\partial {}^{W}{\mathit{\boldsymbol{o}}}_{i}} \right]^{\rm T} $,假设$ \mathit{\boldsymbol{X}} $为$ \mathit{\boldsymbol{A}} $的特征向量矩阵,$ \lambda_{3} $为其最小特征值,$ \mathit{\boldsymbol{x}}_{3} $是对应的特征向量,参考文[20]可求得:
$$ \begin{align*} \label{eq25} \frac{\partial {\mathit{\boldsymbol{n}}}}{\partial {}^{W}{\mathit{\boldsymbol{o}}}_{i}} ={\mathit{\boldsymbol{X}}} \begin{bmatrix} {{\mathit{\boldsymbol{Q}}}_{1, 3}^{{\mathit{\boldsymbol{o}}}_{i}}} \\ {{\mathit{\boldsymbol{Q}}}_{2, 3}^{{\mathit{\boldsymbol{o}}}_{i}}} \\ {{\mathit{\boldsymbol{Q}}}_{3, 3}^{{\mathit{\boldsymbol{o}}}_{i}}} \end{bmatrix} \end{align*} $$ $$ \begin{align} {\mathit{\boldsymbol{Q}}}_{m, 3}^{{\mathit{\boldsymbol{o}}}_{i}} & = \begin{cases} \dfrac{({}^{W}{\mathit{\boldsymbol{o}}}_{i} -{\mathit{\boldsymbol{c}}})^{\rm T}}{N(\lambda_{3} -\lambda_{m})}({{\mathit{\boldsymbol{x}}}_{m} {\mathit{\boldsymbol{n}}}^{\rm T}+{\mathit{\boldsymbol{nx}}}_{m}^{\rm T}}), & m\ne 3 \\ {\mathit{\boldsymbol{0}}}_{1\times 3} , & m=3 \end{cases} \\ \frac{\partial {\mathit{\boldsymbol{c}}}}{\partial {}^{W}{\mathit{\boldsymbol{o}}}_{i}} & =\text{diag }\left(\frac{1}{N}, \frac{1}{N}, \frac{1}{N}\right) \end{align} $$ (24) 则$ {\mathit{\boldsymbol{n}}} $和$ {\mathit{\boldsymbol{c}}} $的协方差矩阵$ \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{n}}}, {\mathit{\boldsymbol{c}}}} $为
$$ \begin{align} \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{n}}}, {\mathit{\boldsymbol{c}}}} =\sum\limits_{i=1}^N \frac{\partial {\mathit{\boldsymbol{f}}}}{\partial {}^{W}{\mathit{\boldsymbol{o}}}_{i}} \mathit{\boldsymbol{\varSigma}}_{^{W}{\mathit{\boldsymbol{o}}}_{i}} \left(\frac{\partial {\mathit{\boldsymbol{f}}}}{\partial {}^{W}{\mathit{\boldsymbol{o}}}_{i}}\right)^{\rm T} \end{align} $$ (25) 1.4 方法实现
为了基于目标检测不确定性模型获得最终的检测结果,需要先对整体网络进行训练,网络结构参考文[3]的训练部分,使用的网络包括目标检测不确定性模型中包含的先验网络、上下文编码器以及预测网络,还添加了一个参数化识别网络。不同的是,在训练阶段,为了保证预训练模型的可靠性,同样将LiDAR测量噪声考虑进来。在给定$ {}^{L}O $及其标注的边界框的前提下,假设存在真实的后验分布$ q(r|G, {}^{L}O+\delta_{^{L}O}) $,使用参数化识别网络学习服从高斯分布的后验分布$ q(r'|G, {}^{L}O+\delta_{^{L}O}) $,表示为$ \mathcal N (\mu_{r} ', \sigma_{r}^{\prime 2}) $,以正则化$ p(r|{}^{L}O+\delta_{^{L}O}) $,$ p(r|{}^{L}O+\delta_{^{L}O}) $应接近于$ q(r'|G, {}^{L}O+\delta_{^{L}O}) $。归一化处理通过边界框的对角线实现。损失函数包含两部分,一部分是预测和回归目标的Huber损失及方向分类的二元交叉熵损失,另一部分是先验网络和识别网络所得到的先验分布$ {\mathcal N}(\mu_{r}, \sigma_{r}^{2}) $和后验分布$ {\mathcal N}(\mu_{r}', \sigma_{r}^{\prime 2}) $中采样的$ r $和$ r' $之间的KL(Kullback-Leibler)散度,通过最小化KL散度来正则化$ r $的分布。利用训练得到的模型,结合目标检测不确定性模型,可以得到相应的可靠检测结果。
在基于MOT不确定性模型进行数据关联时,为了在精度和速度之间实现更好的平衡,采用CA运动模型来预测未来状态。对于每个前一时刻的完整跟踪状态$ {\mathit{\boldsymbol{T}}}_{t-1}^{j} $,通过式(26) 中的CA运动模型估计离散时间$ t $上可能的当前状态$ \hat{\mathit{\boldsymbol{T}}}_{t}^{j} $。为了提高效率,使用卡尔曼滤波(KF)算法来优化预测状态。其对应的误差协方差$ {\mathit{\boldsymbol{P}}} $由式(27) 预测。
$$ \begin{align} \hat{\mathit{\boldsymbol{T}}}_{t}^{j} & ={\mathit{\boldsymbol{FT}}}_{t-1}^{j} \end{align} $$ (26) $$ \begin{align} \hat{\mathit{\boldsymbol{P}}}_{t}^{j} & ={\mathit{\boldsymbol{FP}}}_{t-1}^{j} {\mathit{\boldsymbol{F}}}^{\rm T}+{\mathit{\boldsymbol{Q}}} \end{align} $$ (27) $$ \begin{align} {\mathit{\boldsymbol{F}}} & =\begin{bmatrix} {{\mathit{\boldsymbol{I}}}_{3\times 3}} & {\varepsilon {\mathit{\boldsymbol{I}}}_{3\times 3}} & {\dfrac{1}{2}\varepsilon^{2}{\mathit{\boldsymbol{I}}}_{3\times 3}} & \\ {\mathit{\boldsymbol{0}}_{3\times 3}} & {{\mathit{\boldsymbol{I}}}_{3\times 3}} & {\varepsilon {\mathit{\boldsymbol{I}}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{9\times m}} \\ {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {{\mathit{\boldsymbol{I}}}_{3\times 3}} & \\ & {\mathit{\boldsymbol{0}}_{m\times 9}} & & {{\mathit{\boldsymbol{I}}}_{m\times m}} \end{bmatrix} \end{align} $$ (28) 式(28) 中的$ {\mathit{\boldsymbol{F}}} $为状态转移矩阵,$ {\mathit{\boldsymbol{I}}} $和$ {\mathit{\boldsymbol{0}}} $分别表示单位矩阵和零矩阵,$ \varepsilon $为LiDAR传感器的扫描时间间隔,$ m=4+n $为其他跟踪元素(方向角、高、长、宽、深度特征)的数量,$ {\mathit{\boldsymbol{Q}}}\in \mathbb{R}^{W^{\rm T}\times W^{\rm T}} $是状态函数的协方差矩阵,$ {\mathit{\boldsymbol{P}}}_{t-1} \in \mathbb{R}^{W^{\rm T}\times W^{\rm T}} $为$ t-1 $时刻的误差协方差,$ \hat{\mathit{\boldsymbol{P}}}_{t} \in \mathbb{R}^{W^{\rm T}\times W^{\rm T}} $为$ t $时刻的预测误差协方差。根据状态函数式(26),每个物体的位置$ \mathit{\boldsymbol{p}} $和速度$ \mathit{\boldsymbol{v}} $可分别由式(29) 和式(30) 预测。
$$ \begin{align} \hat{\mathit{\boldsymbol{p}}}_{t}^{j} & ={\mathit{\boldsymbol{p}}}_{t-1}^{j} +\varepsilon {\mathit{\boldsymbol{v}}}_{t-1}^{p, j} +\frac{1}{2}{\mathit{\boldsymbol{a}}}_{t-1}^{p, j} \varepsilon^{2} \end{align} $$ (29) $$ \begin{align} \hat{\mathit{\boldsymbol{v}}}_{t}^{p, j} & ={\mathit{\boldsymbol{v}}}_{t-1}^{p, j} +{\mathit{\boldsymbol{a}}}_{t-1}^{p, j} \varepsilon \end{align} $$ (30) 其中,$ \hat{\mathit{\boldsymbol{p}}}_{t}^{j} $和$ \hat{\mathit{\boldsymbol{v}}}_{t}^{p, j} $分别为预测的位置和速度。
在基于检测的跟踪范式中,通过数据关联可以得到成功匹配的检测和轨迹。在观测更新过程中,对于这些匹配成功的轨迹,通过与观测数据进行比较来校正预测的目标状态,减小轨迹的不确定性。卡尔曼滤波器更新第$ j $条轨迹的具体过程如下:
$$ \begin{align} {\mathit{\boldsymbol{K}}}_{t} & =\hat{\mathit{\boldsymbol{P}}}_{t}^{j} {\mathit{\boldsymbol{H}}}^{\rm T}({\mathit{\boldsymbol{H\hat{P}}}_{t}^{j} {\mathit{\boldsymbol{H}}}^{\rm T}+{\mathit{\boldsymbol{R}}}})^{-1} \end{align} $$ (31) $$ \begin{align} {\mathit{\boldsymbol{T}}}_{t}^{j} & =\hat{\mathit{\boldsymbol{T}}}_{t}^{j} +{\mathit{\boldsymbol{K}}}_{t} ({{\mathit{\boldsymbol{D}}}_{t}^{i} -\mathit{\boldsymbol{H}}\hat{{T\mathit{\boldsymbol{}}}}_{t}^{j}}) \end{align} $$ (32) $$ \begin{align} {\mathit{\boldsymbol{P}}}_{t}^{j} & =({{\mathit{\boldsymbol{I}}}-{\mathit{\boldsymbol{K}}}_{t} {\mathit{\boldsymbol{H}}}})\hat{\mathit{\boldsymbol{P}}}_{t}^{j} \end{align} $$ (33) 其中$ {\mathit{\boldsymbol{R}}} $表示测量噪声的协方差矩阵,$ {\mathit{\boldsymbol{H}}} $表示观测模型,$ {\mathit{\boldsymbol{D}}}_{t}^{i} $是与$ {\mathit{\boldsymbol{T}}}_{t}^{j} $成功关联的检测结果。
与其他方法不同,本文方法在预测步骤中考虑自身定位的准确性对目标状态预测的影响。如果自身定位准确,则预测结果可以提供较为准确的跟踪估计$ {\mathit{\boldsymbol{T}}}_{0} $来初始化轨迹。假设在当前时间步存在较大的目标加速度,那么仅依据初始跟踪状态将难以进行估计。考虑到此时跟踪估计结果$ {\mathit{\boldsymbol{T}}}_{0} $完全来自于检测结果$ {\mathit{\boldsymbol{D}}}_{0} $,因此无法考虑到速度状态估计。在这种情况下,在预测下一个速度时应该会有很大的不确定性。但是如果不在位置预测方程中加入加速度噪声,那么在预测下一个位置时就只有很小的不确定性。所以通过在位置预测中加入额外的加速度不确定性,就会增大位置预测方差,表达更大的不确定性,使数据关联在匹配时变得更加宽松、鲁棒。通过考虑自身定位误差的传递,可以更准确地初始化和跟踪目标的速度与加速度协方差。具体而言,自身定位误差通过过程噪声项反映到目标的速度和加速度方差中,对应的过程协方差矩阵为
$$ \begin{align} {\mathit{\boldsymbol{Q}}}_{k} =[ \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{D}}}_{\text{loc}}}; \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{x}}}_{\text{vel}}};\mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{x}}}_{\text{acc}}};\mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{D}}}_{\text{other}}} ] \end{align} $$ (34) 其中,对角矩阵$ \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{D}}}_{\text{loc}}} $和$ \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{D}}}_{\text{other}}} $表示目标位置和形状参数的预测方差,可以通过概率检测模型得到。矩阵中间的$ \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{x}}}_{\text{vel}}} $和$ \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{x}}}_{\text{acc}}} $表示目标在各轴上的速度和加速度预测方差,它们与自身定位误差相关。过程噪声协方差矩阵$ {\mathit{\boldsymbol{Q}}}_{k} $全面地反映了过程噪声对目标运动预测的影响,使得定位误差能够很好地表示预测中不确定性的来源。
在观测更新步骤中,自身定位误差会对跟踪性能产生更显著的影响。自身定位如果存在误差,将会导致观测数据与预测状态之间存在较大偏差,从而影响滤波算法的更新过程。通过考虑自身定位状态$ {\mathit{\boldsymbol{x}}} $及其方差$ \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{x}}}} $,基于目标检测框$ {\mathit{\boldsymbol{D}}}_{B}^{i} $,利用运动学依赖性$ {\mathit{\boldsymbol{D}}}_{W}^{i} ={\mathit{\boldsymbol{T}}}_{B}^{W} {\mathit{\boldsymbol{D}}}_{B}^{i} $可以得到世界坐标系下的$ {\mathit{\boldsymbol{D}}}_{W}^{i} $及其方差$ {\mathit{\boldsymbol{\varSigma}}}_{{\mathit{\boldsymbol{D}}}_{W}} $,其中考虑了自身定位方差对观测权重的调节作用。具体而言,通过将自身定位的位置分量方差$ {\mathit{\boldsymbol{\varSigma}}}_{{\mathit{\boldsymbol{x}}}_{t}} $与目标跟踪的位置分量方差$ \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{D}}}_{B}} $融合得到:
$$ \begin{align} {\mathit{\boldsymbol{D}}}_{W}' ={\mathit{\boldsymbol{x}}}_{t} +{\mathit{\boldsymbol{D}}}_{B}' \end{align} $$ (35) 其中,$ {\mathit{\boldsymbol{D}}}_{W}' $和$ {\mathit{\boldsymbol{D}}}_{B}' $表示世界坐标系和雷达坐标系下跟踪的目标位置分量,即:
$$ \begin{equation} \mu_{{\mathit{\boldsymbol{D}}}_{W}'} =\mu_{{\mathit{\boldsymbol{x}}}_{t}} +\mu_{{\mathit{\boldsymbol{D}}}_{B}'}, \quad \sigma_{{\mathit{\boldsymbol{D}}}_{W}'}^{2} =\sigma_{{\mathit{\boldsymbol{x}}}_{t}}^{2} +\sigma_{{\mathit{\boldsymbol{D}}}_{B}'}^{2} \end{equation} $$ (36) 将这一方差纳入观测方差矩阵$ {\mathit{\boldsymbol{R}}} $,调节观测权重的计算,实现更可靠的数据融合。因此,为了在卡尔曼滤波中获得准确的多目标跟踪结果,自身定位的准确性在观测更新步骤中显得尤为重要。
本方法采用了一种类似于FAST-LIO2[10]的迭代扩展卡尔曼滤波器,在利用激光雷达和IMU的测量数据进行融合时,通过对IMU数据进行预积分,得到自身定位状态的预测值以及相应的协方差信息。该先验值将与匹配的点-面距离融合,形成最大后验估计值。在基于点-面匹配的建图过程中,为构建位姿估计和点-面匹配约束,LiDAR新扫描帧中的点与体素地图采用直接法进行匹配计算。在SLAM概率平面模型的基础上,对于利用先验位姿得到的世界坐标系下的LiDAR点$ ^{W}o_{i} $,通过哈希函数散列到哈希表中,其中哈希索引通过Faster-LIO空间索引算法[21]根据公式计算:
$$ \begin{align} {\mathit{\boldsymbol{p}}} & = [ p_{x}, p_{y}, p_{z}]^{\rm T}, \quad {\mathit{\boldsymbol{v}}}=\frac{1}{s}[ p_{x}, p_{y}, p_{z}]^{\rm T} \end{align} $$ (37) $$ \begin{align} p_{\mathit{\boldsymbol{v}}} & = h({\mathit{\boldsymbol{v}}}) = ({{\mathit{\boldsymbol{v}}}_{x} {\mathit{\boldsymbol{n}}}_{x}})\text{xor}({{\mathit{\boldsymbol{v}}}_{y} {\mathit{\boldsymbol{n}}}_{y}}){\text{xor}} ({{\mathit{\boldsymbol{v}}}_{z} {\mathit{\boldsymbol{n}}}_{z}}) \mod N \end{align} $$ (38) 其中,$ p_{\mathit{\boldsymbol{v}}} $是$ ^{W}o_{i} $在哈希表中的索引,$ h(\cdot) $表示哈希函数,$ p_{x}, p_{y}, p_{z} $是点$ {\mathit{\boldsymbol{p}}}\in \mathbb{R}^{3} $的坐标值。$ s $是体素尺寸,$ n_{x}, n_{y}, n_{z} $是大的质数,$ N $是哈希表的大小。具体而言,通过构建的基于八叉树的动态管理体素的空间划分结构,八叉树的叶节点保存体素地址。同时,设计一个以哈希索引为键、体素指针为值的哈希表。通过该组合结构,可以快速查找点所属体素并遍历周围近邻体素。通过高效地找到其所在根体素,计算该点到根体素下所有子体素的平面之间的距离来寻找可能的匹配:
$$ \begin{align} d_{i} ={\mathit{\boldsymbol{n}}}_{i}^{\rm T} ({}^{W}{\mathit{\boldsymbol{o}}}_{i} -{\mathit{\boldsymbol{c}}}_{i}) \end{align} $$ (39) $ {\mathit{\boldsymbol{n}}}_{i} $和$ \mathit{\boldsymbol{c}}_{i} $代表子体素所含平面的法向量和中心位置。而$ {\mathit{\boldsymbol{n}}}_{i} $、$ \mathit{\boldsymbol{c}}_{i} $和LiDAR点$ ^{W}o_{i} $都存在不确定性。将这些不确定性都纳入考虑,得到:
$$ \begin{align} d_{i} &= ({{\mathit{\boldsymbol{n}}}_{i}^{\mathrm{gt}}+{\mathit{\boldsymbol{\boldsymbol\delta}}}_{{\mathit{\boldsymbol{n}}}_{i}}})^{\rm T} [ ({{}^{W}{\mathit{\boldsymbol{o}}}_{i}^{\mathrm{gt}} +{\mathit{\boldsymbol{\boldsymbol\delta}}}_{^{W}{\mathit{\boldsymbol{o}}}_{i}}})-{\mathit{\boldsymbol{c}}}_{i}^{\mathrm{gt}} -{\mathit{\boldsymbol{\boldsymbol\delta}}}_{{\mathit{\boldsymbol{c}}}_{i}}] \\ & \approx \underbrace{{\mathit{\boldsymbol{n}}}_{i}^{\mathrm{gtT}}({{}^{W}{\mathit{\boldsymbol{o}}}_{i}^{\mathrm{gt}} -{\mathit{\boldsymbol{c}}}_{i}^{\mathrm{gt}}})}_0 + \underbrace{{\mathit{\boldsymbol{J}}}_{{\mathit{\boldsymbol{n}}}_{i}} {\mathit{\boldsymbol{\boldsymbol\delta}}}_{{\mathit{\boldsymbol{n}}}_{i}} +{\mathit{\boldsymbol{J}}}_{{\mathit{\boldsymbol{c}}}_{i}} {\mathit{\boldsymbol{\boldsymbol\delta}}}_{{\mathit{\boldsymbol{c}}}_{i}} +{\mathit{\boldsymbol{J}}}_{^{W}{\mathit{\boldsymbol{o}}}_{i}} {\mathit{\boldsymbol{\boldsymbol\delta}}}_{^{W}{\mathit{\boldsymbol{o}}}_{i}}}_{m_{i}} \end{align} $$ (40) 即:
$$ \begin{align} d_{i} \sim {\mathcal N}(0, \varSigma_{m_{i}}), \quad \varSigma_{m_{i}} ={\mathit{\boldsymbol{J}}}_{m_{i}} \boldsymbol \varSigma_{{\mathit{\boldsymbol{n}}}_{i}, {\mathit{\boldsymbol{c}}}_{i}, {}^{W}{\mathit{\boldsymbol{o}}}_{i}} {\mathit{\boldsymbol{J}}}_{m_{i}}^{\rm T} \end{align} $$ (41) 其中,
$$ \begin{gather} {\mathit{\boldsymbol{J}}}_{m_{i}} =[ {\mathit{\boldsymbol{J}}}_{{\mathit{\boldsymbol{n}}}_{i}}, {\mathit{\boldsymbol{J}}}_{{\mathit{\boldsymbol{c}}}_{i}}, {\mathit{\boldsymbol{J}}}_{^{W}{\mathit{\boldsymbol{o}}}_{i}} ]=[ ({{}^{W}{\mathit{\boldsymbol{o}}}_{i} -{\mathit{\boldsymbol{c}}}_{i}})^{\rm T}, -{\mathit{\boldsymbol{n}}}_{i}^{\rm T}, {\mathit{\boldsymbol{n}}}_{i}^{\rm T}] \end{gather} $$ (42) $$ \begin{gather} \mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{n}}}_{i}, {\mathit{\boldsymbol{c}}}_{i}, {}^{W}{\mathit{\boldsymbol{o}}}_{i}} = \begin{bmatrix} {\mathit{\boldsymbol{\varSigma}}_{{\mathit{\boldsymbol{n}}}_{i}, {\mathit{\boldsymbol{c}}}_{i}}} & {\mathit{\boldsymbol{0}}} \\ {\mathit{\boldsymbol{0}}} & {\mathit{\boldsymbol{\varSigma}}_{^{W}{\mathit{\boldsymbol{o}}}_{i}}} \end{bmatrix} \end{gather} $$ (43) 若点在候选平面上,点-面距离$ d_{i} $需要服从式(41) 中的分布。对于分布的标准差$ \sigma =\sqrt{\varSigma_{m_{i}}} $,设定满足点-面距离在$ 3\sigma $以内为有效匹配;如果一个点可以匹配多个平面,则选取匹配概率最高的平面;若不满足$ 3\sigma $距离设定,则丢弃该点,防止体素量化导致的假匹配。
优化后的前景目标检测与跟踪可以提高建图匹配的置信度,获得方差更小的观测分布$ \varSigma_{m_{i}} $,这增强了式(41) 对状态估计的客观约束,有利于提高建图的一致性和准确性。此外,根据动态物体周围点的信息,通过降低点-面距离判断的有效阈值来降低误匹配。具体而言,将动态点云周围点的距离阈值$ \theta_{d_{i}} $设定为$ \sigma $,其余点保留$ 3\sigma $判定:
$$ \begin{align} \theta_{d_{i}} =\begin{cases} \sigma, & p_{i} \in p' \\ 3\sigma, & \text{其他} \end{cases} \end{align} $$ (44) 其中$ p'= g ({{\mathit{\boldsymbol{T}}}_{x} \pm {\mathit{\boldsymbol{T}}}_{\rm s}}) $为动态目标周围的点云,$ g(\cdot) $表示邻域搜索,$ {\mathit{\boldsymbol{T}}}_{x} $和$ {\mathit{\boldsymbol{T}}}_{\rm s} $分别是跟踪目标的位置和形状分量。通过判定体素地图中动态点云所映射的哈希索引与当前扫描帧的哈希索引一致,进而得到动态目标位置的邻域体素。综上所述,优化后的前景跟踪可以提高匹配观测的确定性,增强测量模型约束,从而有利于整体位姿估计;而自身定位误差也会通过过程噪声影响目标位置的预测,体现出定位与多目标跟踪任务相互影响促进的关系。
需要说明的是,本文当前主要针对典型的室外结构化道路场景进行方法验证,运动目标较为规律,地面较为平坦。当遇到复杂的室内场景或目标运动规律复杂时,方法的适用性还有待进一步扩展。
2. 实验(Experiment)
实验环境是在Ubuntu 18.04和ROS下,硬件配置为一台i7 CPU、16 GB内存的笔记本电脑。
数据集 为了验证方法的有效性并确保实验的可靠性,分别基于开源的KITTI[22]和UrbanNav[23]数据集进行动态场景的实验。其中,KITTI数据集提供了完整的激光雷达扫描和IMU数据。评估选择了包含移动物体的序列。64光束激光雷达扫描仪(Velodyne HDL-64E)平均每秒提供10次扫描,IMU传感器(OxTS RT3003)平均每秒提供100条记录。采用预训练的GLENet模型[2]检测点云中的3维物体。UrbanNav数据集是在香港的城市高楼区收集的数据集,场景周边具有许多高耸的建筑物且动态目标多。因此在实验时,主要采用具有代表性的HK-Medium-Urban以及HK-Deep-Urban这2个数据集对本文方法进行评估,从而验证算法在大规模复杂动态环境下的建图可靠性。
评价指标 由于目前还没有公开的同时考虑了SLAM、目标检测和跟踪的多任务感知数据集,为全面评估算法性能,实验结果分为2个部分进行评估。定位精度方面,采用EVO工具对算法结果进行评估,包括关注全局一致性的绝对轨迹误差(ATE)和关注局部一致性的相对姿态误差(RPE)2个指标。ATE能够反映整体定位精度,但无法揭示系统在特定区域的表现。与之相对,RPE则能更细致地评估系统在局部区域的定位性能。RPE主要分析相邻帧之间的误差变化,能够评价姿态估计的实时性能。除此之外,为了更全面地反映误差情况,在实验对比结果中不仅采用了均方根误差(RMSE),同时还将误差均值(mean)、误差中位数(median)、误差平方和(SSE)以及标准差(STD)列入对比项,通过多个指标的详细对比来证明算法的可靠性与鲁棒性。同时也通过稠密建图质量的定性表示,侧面说明定位的准确性。对于前景感知中的检测与跟踪,采用KITTI数据集的评估指标来评估多目标跟踪性能。这些常用指标包括MOTA(multiple object tracking accuracy)和高阶跟踪准确性(HOTA[24]),综合了3个主要误差来源:误报、漏报和身份切换(IDSW),同时重点考虑IDSW,以验证跟踪器使预测轨迹和对应目标长时间保持对应关系的能力。
1) 环境建图精度及一致性
该实验主要评估了所提出的多任务感知方法中SLAM模块在位姿估计和建图一致性方面的性能表现,并与当前最先进的4D-SLAM、FAST-LIO2等算法进行对比。局部地图尺寸选为1 000 m,激光雷达原始点经过降采样后直接输入状态估计。在所有实验中,空间降采样分辨率均设为0.5 m。本文方法的体素地图的最大层数设置为4层,每层体素由8个子邻域体素组成,体素内的平面阈值为0.01。
在KITTI Odometry数据集的所有序列上,3种方法的ATE结果如表 1所示。从整体上看,根据5种不同的指标,本方法几乎在所有序列上都具有优势,综合性能得到极大提升。
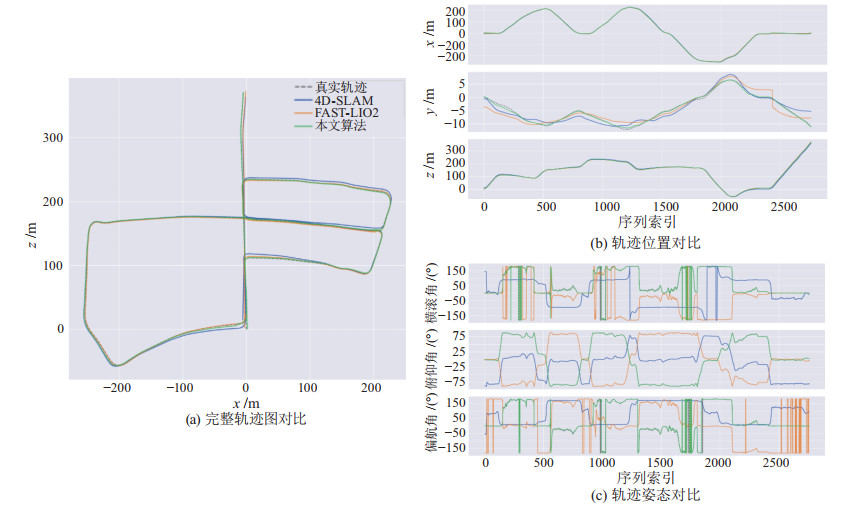
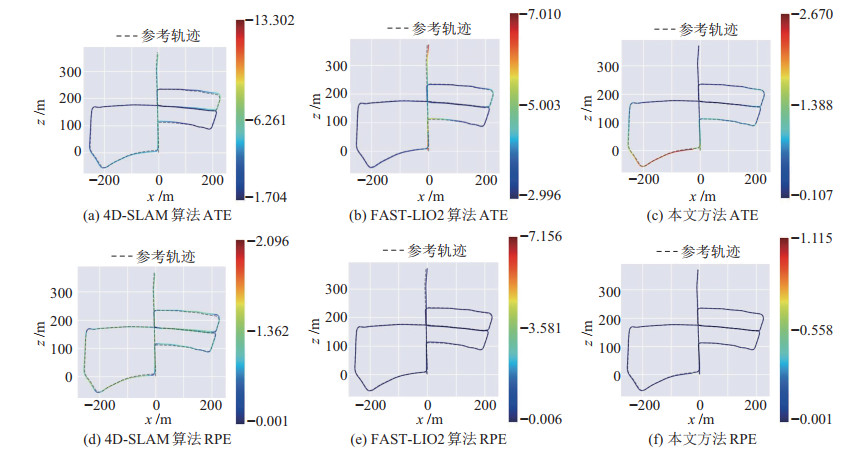
表 1 在KITTI Odometry数据集所有序列上的ATE结果对比(单位:m)Table 1. Comparison of ATE results on all sequences in KITTI Odometry dataset (unit: m)指标 00 01 02 04 05 06 07 08 09 10 4D-SLAM 均值 12.06 24.95 16.99 7.65 3.09 2.46 2.22 4.07 2.38 25.66 中位数 11.18 26.32 18.02 8.15 2.83 2.83 2.17 3.98 2.49 27.03 RMSE 5.84 27.72 18.85 7.86 3.53 2.70 2.36 4.38 2.51 28.55 平方和 6.14e+4 8.33e$ + $5 3.67e$ + $5 9029.34 3.44e$ + $4 8041.84 6124.38 7.80e$ + $4 1.00e$ + $5 1.82e$ + $5 标准差 4.04 12.08 8.16 0.43 1.70 1.13 0.80 1.61 0.79 5.21 FAST-LIO2 均值 4.57 26.05 7.75 3.18 3.77 3.36 3.21 5.02 3.45 3.44 中位数 3.48 25.52 7.64 2.76 3.38 3.15 3.09 4.85 3.46 3.34 RMSE 5.62 28.28 8.30 3.65 3.86 3.40 3.22 5.22 3.49 3.48 平方和 1.43e$ + $5 8.81e$ + $5 3.21e$ + $5 3600.55 4.12e$ + $4 1.27e$ + $4 1.14e$ + $4 1.11e$ + $5 1.94e$ + $4 1.46e$ + $4 标准差 3.28 11.02 2.99 1.78 0.84 0.54 0.27 1.41 0.52 0.51 本文算法 均值 3.84 6.17 7.52 1.80 0.82 0.36 0.76 2.68 2.26 0.71 中位数 3.99 6.20 6.69 1.80 0.70 0.25 0.87 2.40 1.44 0.62 RMSE 4.07 6.42 8.14 1.80 1.02 0.47 0.82 3.05 2.86 0.82 平方和 7.51e+4 4.53e+4 3.09e+5 876.08 2858.11 240.51 745.24 3.79e+4 1.30e+4 800.13 标准差 1.33 1.75 3.11 0.01 0.61 0.30 0.32 1.46 1.76 0.41 3种方法在KITTI数据集05序列上的ATE和RPE详细对比结果如表 2所示,整体建图效果和轨迹对比结果如图 7、图 8所示,ATE和RPE整体轨迹误差结果如图 9所示。3种方法对比表明,本文方法的误差均为最小。这一显著优势表明,本文方法能够提供准确的数据关联,并在动态场景等挑战性情况下保持稳定的位姿估计。
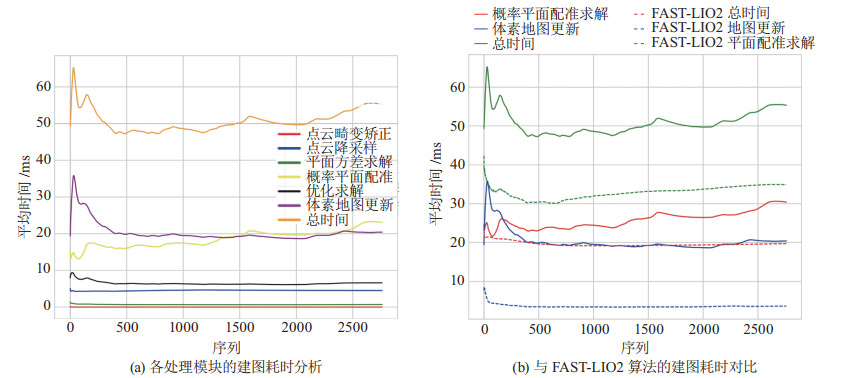
表 2 KITTI Odometry数据集05序列去除动态物体后ATE和RPE对比结果(单位:m)Table 2. Comparative results of ATE and RPE after removing dynamic objects on sequence 05 in KITTI Odometry dataset (unit: m)评估指标 4D-SLAM FAST-LIO2 本文方法 ATE.mean 3.09 3.77 0.82 ATE.median 2.83 3.38 0.70 ATE.RMSE 3.53 3.86 1.02 ATE.SSE 3.44e$ + $4 4.12e$ + $4 2858.11 ATE.STD 1.70 0.84 0.61 RPE.mean 0.07 0.07 0.02 RPE.median 0.06 0.05 0.01 RPE.RMSE 0.08 0.15 0.04 RPE.SSE 4.70 73.89 4.22 RPE.STD 0.03 0.15 0.03 在UrbanNav的2个数据集上,地图重建结果的局部细节如图 10和图 11所示。由图可见,多任务感知方法的建图结果中,因为去除了运动目标的影响,运动目标造成的拖影及多余杂点都已被移除,得到了准确且无噪的高精度地图。在计算效率方面,所提方法将点云建模为概率体素地图,避免了实时或定期建立KD(K-dimensional)树的需求。KD树搜索邻近点的时间复杂度为$ O(m \log n) $,其中$ m $是维度,$ n $是点云地图中的点数。相比之下,在体素地图中搜索相邻平面的复杂度接近$ O(1) $,从而确保了方法的实时性,但是需要额外计算每个点和平面的概率分布。图 12比较了本文方法与FAST-LIO2方法在KITTI 05序列上的运行时间。结果表明,尽管计算点云和平面概率分布需要额外的计算时间,但得到的概率信息可以有效剔除测量中的异常值。同时,优化所增加的时间开销仅约为10 ms,基本可以满足实时性要求。需要注意的是,随着传感器的移动,全局体素地图的规模也会逐渐增大,优化时间开销也会有所增加。
2) 目标检测与跟踪实验
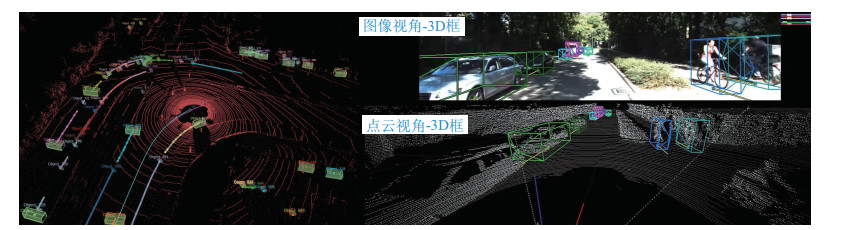
利用多任务感知方法中的目标检测与跟踪模块在KITTI的3D目标检测和跟踪数据集上进行动态物体的检测跟踪实验,以此确保MOT实现的准确性和可靠性。如图 13所示,可以检测的对象包括车辆、行人、骑自行车的人等,在检测的基础上进行多目标跟踪,可以为检测目标分配ID以标明不同的物体,并可以实现精确跟踪。在超参数配置方面,4D-SLAM和CenterTube算法采用原文中的默认配置;本文设置最大预测次数为12,初始化的最大预测次数为2。
通过采用GLENet检测器[3],本方法在汽车验证集上进行前景跟踪时的MOTA指标达到84.64%,比4D-SLAM算法的跟踪结果高出11.54%,需要注意的是,4D-SLAM算法的跟踪耗时只统计了单一模块,而本文方法计算的是协同感知的时间开销。与CenterTube算法[9]相比,本方法的HOTA指标也高出7.7%。需要注意的是,这里CenterTube算法同样使用的是基于体素的目标检测器,在KITTI MOT数据集中的结构化道路场景和目标运动规律单一的场景下,性能没有明显差异。表 3展示了本文方法和4D-SLAM以及CenterTube算法在关键指标上的统计数据,本文方法显示出一定的性能优越性。此外,对于IDSW这个重要指标,本文方法也是最佳。请注意,IDSW数值(30)评估结果相对稳定在较高水平。这一显著优势表明,在变化相对较大的环境中,以及在数据采集车经常移动的情况下,本文方法能够实现准确的数据关联,能够通过预测跟踪来补偿2帧之间的位移距离,从而保持持续稳定的跟踪能力,表现出极大的优越性。
表 3 KITTI MOT Car测试集上的多目标跟踪结果对比Table 3. Comparison of multi-object tracking performance on KITTI MOT Car test datasetMOTA /%$ \uparrow $ HOTA /%$ \uparrow $ IDSW $ \downarrow $ FPS $ \uparrow $ CenterTube 81.56 67.76 737 8.1 4D-SLAM 73.1 N/A N/A 25 本文方法 84.64 75.46 30 14.3 3) 消融实验
为验证前景感知对背景SLAM的影响,实验在KITTI Odometry数据集的所有序列上,对启用前景感知(wMOT)和不启用前景感知(woMOT)两种模式进行了对比评估。评估指标采用绝对轨迹误差(ATE)。
表 4结果表明,启用前景感知时,绝大多数情况下轨迹估计的精度要优于不启用前景感知时。这表明对于大规模复杂场景来说,多任务感知不仅实现了前景目标的可靠检测,同时对建图精度和一致性也是十分重要的。
表 4 KITTI Odometry数据集上启动前景感知模块前后的ATE对比(单位:m)Table 4. Comparison of ATE with or without foreground perception module on KITTI Odometry dataset (unit: m)序列 均值 中位数 RMSE 平方和 标准差 woMOT wMOT woMOT wMOT woMOT wMOT woMOT wMOT woMOT wMOT 00 4.67 3.84 4.20 3.99 5.32 4.07 1.29e$ + $5 7.51e+4 2.56 1.33 01 5.65 6.17 5.55 6.20 5.87 6.42 3.79e+4 4.53e$ + $4 1.59 1.75 02 22.49 7.52 15.96 6, 69 39.30 8.14 7.20e$ + $6 3.09e+5 32.23 3.11 04 1.85 1.80 1.85 1.80 1.85 1.80 932.36 876.08 0.01 0.01 05 0.97 0.82 0.83 0.70 1.20 1.02 4003.23 2858.11 0.71 0.61 06 1.02 0.36 0.90 0.25 1.09 0.47 1301.65 240.51 0.38 0.30 07 0.80 0.76 0.82 0.87 0.84 0.82 783.85 745.24 0.27 0.32 08 2.59 2.68 2.36 2.40 2.93 3.05 3.50e+4 3.79e$ + $4 1.38 1.46 09 3.76 2.26 2.41 1.44 4.72 2.86 3.54e$ + $4 1.30e+4 2.85 1.76 10 1.02 0.71 1.07 0.62 1.10 0.82 1454.27 800.13 0.42 0.41 为验证多任务协同对单任务时间的影响,在KITTI Odometry数据集上对启用与不启用前景感知的情形进行多任务协同前后各任务的平均执行时间对比实验。如表 5所示,多任务协同虽增加了调度协调的时间开销,但各个任务的实时性能仍满足要求。
表 5 KITTI Odometry数据集上多任务协同时间开销分析的对比结果(单位:ms)Table 5. Comparison results of multitask collaboration time overhead analysis on KITTI Odometry dataset (unit: ms)仅背景建图 仅前景感知 协同感知 平均耗时 26.45 61.52 68.77 标准差 9.87 8.10 14.63 为验证背景建图对前景跟踪的影响,在KITTI MOT数据集上进行比较。去除背景建图模块后,前景跟踪模块将自身姿态真值作为输入,进行离线处理。结果如表 6所示,当移除背景建图模块时,虽然HOTA等指标高于联合感知的结果,但前景跟踪的IDSW次数从30大幅增加到225。这说明缺少背景建图提供的定位先验信息,如自身姿态估计值的不确定程度,会降低前景跟踪的鲁棒性。
表 6 KITTI MOT Car验证集上纯感知模块的跟踪性能对比Table 6. Comparison of tracking performance of perception-only modules on KITTI MOT Car validation datasetMOTA /%$ \uparrow $ HOTA /%$ \uparrow $ IDSW$ \downarrow $ 协同感知 84.64 75.46 30 仅前景感知 88.81 77.8 225 3. 结论(Conclusion)
针对复杂动态场景的多任务感知问题,基于动态贝叶斯网络将目标检测、跟踪、定位和建图等多个场景感知子任务统一在后验概率估计的框架下,实现对复杂场景的联合感知建模以及参数估计的不确定性分析。不同于独立处理各子任务的传统方式,本文通过建模各任务的可信度,针对LiDAR测量噪声和位姿估计误差导致的建图与定位不确定性,在体素空间上构建基于直接法匹配的概率平面模型,以此提高建图鲁棒性和定位准确性;同时,针对目标漏检和数据关联不可靠所导致的目标检测跟踪不确定性问题,在目标运动特征的基础上融合自身定位误差构建基于预测置信度的数据关联概率模型,实现对动态目标的准确检测与跟踪。通过迭代优化协同各任务,目标检测结果有助于消除定位建图中的干扰,定位结果也可提升目标跟踪的精确度。在开源数据集KITTI和UrbanNav上进行了大量定性和定量的实验。实验结果表明,基于不确定性建模的多任务感知法在复杂动态环境中取得了显著的性能提升。通过可靠的动态目标检测与跟踪,以及构建一致的静态环境地图,本方法实现了准确的定位,相较于当前最先进的SLAM方法取得显著提升。后续工作将优化模型并提升算法速度,同时扩大方法的适用范围以处理更为复杂的大规模场景。
-
表 1 在KITTI Odometry数据集所有序列上的ATE结果对比(单位:m)
Table 1 Comparison of ATE results on all sequences in KITTI Odometry dataset (unit: m)
指标 00 01 02 04 05 06 07 08 09 10 4D-SLAM 均值 12.06 24.95 16.99 7.65 3.09 2.46 2.22 4.07 2.38 25.66 中位数 11.18 26.32 18.02 8.15 2.83 2.83 2.17 3.98 2.49 27.03 RMSE 5.84 27.72 18.85 7.86 3.53 2.70 2.36 4.38 2.51 28.55 平方和 6.14e+4 8.33e$ + $5 3.67e$ + $5 9029.34 3.44e$ + $4 8041.84 6124.38 7.80e$ + $4 1.00e$ + $5 1.82e$ + $5 标准差 4.04 12.08 8.16 0.43 1.70 1.13 0.80 1.61 0.79 5.21 FAST-LIO2 均值 4.57 26.05 7.75 3.18 3.77 3.36 3.21 5.02 3.45 3.44 中位数 3.48 25.52 7.64 2.76 3.38 3.15 3.09 4.85 3.46 3.34 RMSE 5.62 28.28 8.30 3.65 3.86 3.40 3.22 5.22 3.49 3.48 平方和 1.43e$ + $5 8.81e$ + $5 3.21e$ + $5 3600.55 4.12e$ + $4 1.27e$ + $4 1.14e$ + $4 1.11e$ + $5 1.94e$ + $4 1.46e$ + $4 标准差 3.28 11.02 2.99 1.78 0.84 0.54 0.27 1.41 0.52 0.51 本文算法 均值 3.84 6.17 7.52 1.80 0.82 0.36 0.76 2.68 2.26 0.71 中位数 3.99 6.20 6.69 1.80 0.70 0.25 0.87 2.40 1.44 0.62 RMSE 4.07 6.42 8.14 1.80 1.02 0.47 0.82 3.05 2.86 0.82 平方和 7.51e+4 4.53e+4 3.09e+5 876.08 2858.11 240.51 745.24 3.79e+4 1.30e+4 800.13 标准差 1.33 1.75 3.11 0.01 0.61 0.30 0.32 1.46 1.76 0.41 表 2 KITTI Odometry数据集05序列去除动态物体后ATE和RPE对比结果(单位:m)
Table 2 Comparative results of ATE and RPE after removing dynamic objects on sequence 05 in KITTI Odometry dataset (unit: m)
评估指标 4D-SLAM FAST-LIO2 本文方法 ATE.mean 3.09 3.77 0.82 ATE.median 2.83 3.38 0.70 ATE.RMSE 3.53 3.86 1.02 ATE.SSE 3.44e$ + $4 4.12e$ + $4 2858.11 ATE.STD 1.70 0.84 0.61 RPE.mean 0.07 0.07 0.02 RPE.median 0.06 0.05 0.01 RPE.RMSE 0.08 0.15 0.04 RPE.SSE 4.70 73.89 4.22 RPE.STD 0.03 0.15 0.03 表 3 KITTI MOT Car测试集上的多目标跟踪结果对比
Table 3 Comparison of multi-object tracking performance on KITTI MOT Car test dataset
MOTA /%$ \uparrow $ HOTA /%$ \uparrow $ IDSW $ \downarrow $ FPS $ \uparrow $ CenterTube 81.56 67.76 737 8.1 4D-SLAM 73.1 N/A N/A 25 本文方法 84.64 75.46 30 14.3 表 4 KITTI Odometry数据集上启动前景感知模块前后的ATE对比(单位:m)
Table 4 Comparison of ATE with or without foreground perception module on KITTI Odometry dataset (unit: m)
序列 均值 中位数 RMSE 平方和 标准差 woMOT wMOT woMOT wMOT woMOT wMOT woMOT wMOT woMOT wMOT 00 4.67 3.84 4.20 3.99 5.32 4.07 1.29e$ + $5 7.51e+4 2.56 1.33 01 5.65 6.17 5.55 6.20 5.87 6.42 3.79e+4 4.53e$ + $4 1.59 1.75 02 22.49 7.52 15.96 6, 69 39.30 8.14 7.20e$ + $6 3.09e+5 32.23 3.11 04 1.85 1.80 1.85 1.80 1.85 1.80 932.36 876.08 0.01 0.01 05 0.97 0.82 0.83 0.70 1.20 1.02 4003.23 2858.11 0.71 0.61 06 1.02 0.36 0.90 0.25 1.09 0.47 1301.65 240.51 0.38 0.30 07 0.80 0.76 0.82 0.87 0.84 0.82 783.85 745.24 0.27 0.32 08 2.59 2.68 2.36 2.40 2.93 3.05 3.50e+4 3.79e$ + $4 1.38 1.46 09 3.76 2.26 2.41 1.44 4.72 2.86 3.54e$ + $4 1.30e+4 2.85 1.76 10 1.02 0.71 1.07 0.62 1.10 0.82 1454.27 800.13 0.42 0.41 表 5 KITTI Odometry数据集上多任务协同时间开销分析的对比结果(单位:ms)
Table 5 Comparison results of multitask collaboration time overhead analysis on KITTI Odometry dataset (unit: ms)
仅背景建图 仅前景感知 协同感知 平均耗时 26.45 61.52 68.77 标准差 9.87 8.10 14.63 表 6 KITTI MOT Car验证集上纯感知模块的跟踪性能对比
Table 6 Comparison of tracking performance of perception-only modules on KITTI MOT Car validation dataset
MOTA /%$ \uparrow $ HOTA /%$ \uparrow $ IDSW$ \downarrow $ 协同感知 84.64 75.46 30 仅前景感知 88.81 77.8 225 -
[1] FENG D, HAASE-SCHÜTZ C, ROSENBAUM L, et al. Deep multi-modal object detection and semantic segmentation for autonomous driving: Datasets, methods, and challenges[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 22(3): 1341-1360. doi: 10.1109/TITS.2020.2972974
[2] FAN L, YANG Y X, WANG F, et al. Super sparse 3D object detection[DB/OL]. (2023-01-05)[2023-06-01]. https://arxiv.org/abs/2301.02562.
[3] ZHANG Y F, ZHANG Q J, ZHU Z Y, et al. GLENet: Boosting 3D object detectors with generative label uncertainty estimation[J]. International Journal of Computer Vision, 2023, 131: 3332-3352. doi: 10.1007/s11263-023-01869-9
[4] FENG D, WANG Z N, ZHOU Y Y, et al. Labels are not perfect: Inferring spatial uncertainty in object detection[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(8): 9981-9994. doi: 10.1109/TITS.2021.3096943
[5] PITROPOV M, HUANG C, ABDELZAD V, et al. LiDAR-MIMO: Efficient uncertainty estimation for LiDAR-based 3D object detection[C]//IEEE Intelligent Vehicles Symposium. Piscataway, USA: IEEE, 2022: 813-820. doi: 10.1109/IV51971.2022.9827244
[6] PAN H J, WANG Z N, ZHAN W, et al. Towards better performance and more explainable uncertainty for 3D object detection of autonomous vehicles[C]//IEEE 23rd International Conference on Intelligent Transportation Systems. Piscataway, USA: IEEE, 2020: 1-7. doi: 10.1109/ITSC45102.2020.9294177
[7] WENG X, WANG J, HELD D, et al. 3D multi-object tracking: A baseline and new evaluation metrics[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2020: 10359-10366. doi: 10.1109/IROS45743.2020.9341164
[8] HE J W, FU C Y, WANG X Y. 3D multi-object tracking based on uncertainty-guided data association[DB/OL]. (2023-03-03)[2023-06-01]. https://arxiv.org/abs/2303.01786.
[9] LIU H, MA Y N, HU Q Y, et al. CenterTube: Tracking multiple 3D objects with 4D tubelets in dynamic point clouds[J/OL]. IEEE Transactions on Multimedia, 2023, 25: 8793-8804. doi: 10.1109/TMM.2023.3241548
[10] XU W, CAI Y X, HE D J, et al. FAST-LIO2: Fast direct LiDAR-inertial odometry[J]. IEEE Transactions on Robotics, 2022, 38(4): 2053-2073. doi: 10.1109/TRO.2022.3141876
[11] ARORA M, WIESMANN L, CHEN X, et al. Mapping the static parts of dynamic scenes from 3D LiDAR point clouds exploiting ground segmentation[C]//European Conference on Mobile Robots. Piscataway, USA: IEEE, 2021. doi: 10.1109/ECMR50962.2021.9568799
[12] PARK J, CHO Y, SHIN Y S. Nonparametric background model-based LiDAR SLAM in highly dynamic urban environments[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(12): 24190-24205. doi: 10.1109/TITS.2022.3204917
[13] CHEN X, MILIOTO A, PALAZZOLO E, et al. SuMa++: Efficient LiDAR-based semantic SLAM[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2019: 4530-4537. doi: 10.1109/IROS40897.2019.8967704
[14] PARK C, MOGHADAM P, WILLIAMS J L, et al. Elasticity meets continuous-time: Map-centric dense 3D LiDAR SLAM[J]. IEEE Transactions on Robotics, 2022, 38(2): 978-997. doi: 10.1109/TRO.2021.3096650
[15] BALTASHOV I, SEMAKOVA A, BAKHSHIEV A. 3D SLAM in dynamic environment: An algorithm for mobile robot[C]// 24th International Conference on System Theory, Control and Computing. Piscataway, USA: IEEE, 2020: 642-647. doi: 10.1109/ICSTCC50638.2020.9259761
[16] CHEN Y F, SUN S, YIN H, et al. Exploring the effect of 3D object removal using deep learning for LiDAR-based mapping and long-term vehicular localization[C]//IEEE 25th International Conference on Intelligent Transportation Systems. Piscataway, USA: IEEE, 2022: 1730-1735. doi: 10.1109/ITSC55140.2022.9921969
[17] WANG Z L, LI W Y, SHEN Y, et al. 4-D SLAM: An efficient dynamic Bayes network-based approach for dynamic scene understanding[J]. IEEE Access, 2020, 8: 219996-220014. doi: 10.1109/ACCESS.2020.3042339
[18] WANG Y B, WANG Z L, WU X. An efficient and accurate 3D SLAM method for dynamic environment[C]//4th International Conference on Robotics and Computer Vision. Piscataway, USA: IEEE, 2022: 148-153. doi: 10.1109/ICRCV55858.2022.9953253
[19] YUAN C J, XU W, LIU X Y, et al. Efficient and probabilistic adaptive voxel mapping for accurate online LiDAR odometry[J]. IEEE Robotics and Automation Letters, 2022, 7(3): 8518-8525. doi: 10.1109/LRA.2022.3187250
[20] ROBERT C P, CASELLA G. Monte Carlo statistical methods[M]. New York, USA: Springer, 1999. doi: 10.1007/978-1-4757-4145-2
[21] BAI C G, XIAO T, CHEN Y J, et al. Faster-LIO: Lightweight tightly coupled LiDAR-inertial odometry using parallel sparse incremental voxels[J]. IEEE Robotics and Automation Letters, 2022, 7(2): 4861-4868. doi: 10.1109/LRA.2022.3152830
[22] GEIGER A, LENZ P, URTASUN R. Are we ready for autonomous driving? The KITTI vision benchmark suite[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, USA: IEEE, 2012: 3354-3361. doi: 10.1109/CVPR.2012.6248074
[23] HSU L T, KUBO N, WEN W, et al. UrbanNav: An open-sourced multisensory dataset for benchmarking positioning algorithms designed for urban areas[C]//34th International Technical Meeting of the Satellite Division of the Institute of Navigation. Manassas, USA: ION, 2021: 226-256. doi: 10.33012/2021.17895
[24] LUITEN J, OSEP A, DENDORFER P, et al. HOTA: A higher order metric for evaluating multi-object tracking[J]. International Journal of Computer Vision, 2021, 129: 548-578. doi: 10.1007/s11263-020-01375-2



 下载:
下载: